Geschreven door Maaike Steijlen, Zillah de Groot en Marcella Plukaard

Montessori wiskunde
Maria Montessori interpreteerde wiskunde als een andere manier van communicatie tussen mensen. Met zowel de taal als het begrip van getallen begon de mens zich te organiseren en beschavingen te vormen. Rekenen en taal vormen de basis van alle begrip dat we hebben van deze wereld.
De wiskundige materialen in een Montessorischool zijn betoverende materialen die het kind op een concrete manier naar abstractie leiden. We leggen hen nooit uit hoe de operatie abstract uitgevoerd moet worden. Dit zou de vreugde van het eureka-moment wegnemen. Het gemak waarmee een kind wiskunde kan doen heeft zijn wortels voor de leeftijd van 6 jaar. Met het zintuiglijke materiaal in de onderbouw leggen ze later hun basis voor wiskunde. Het 3 tot 6-jarige kind leert door middel van zintuigen en beweging, Ze leren door het materiaal te manipuleren.
"Geef de geest nooit iets wat niet eerst door de hand is ervaren".
Dr. Maria Montessori
Eenmaal in het de midden- en bovenbouw, hebben de kinderen de verbeelding en de verwondering om verder te verkennen en te bevragen. Natuurlijk hebben alle mensen de neiging om orde, nauwkeurigheid, precisie, schatting, berekening, abstractie, verbeelding en rede te zoeken, maar de leeftijd waarop kinderen echt diepgaand naar antwoorden beginnen te graven is in hun midden- en bovenbouw jaren.
De kralenkast is één materiaal in het bijzonder dat in alle fasen van de Montessorischool wordt gebruikt. Van de onderbouw tot het einde van de basisschool.
Het kralenrek in de onderbouw

Jonge kinderen zijn onder de indruk van de kralenkettingen, van de kleur, de kralen en de ruimte die de kettingen innemen tijdens het werken. De aantrekkelijkheid van het materiaal geeft het kind een intrinsieke motivatie om er vanaf zeer jonge leeftijd mee te werken.
Doordat andere met de kralenkettingen werken, geeft dit de kinderen ook motivatie om naar dit materiaal toe te werken. Want wat is er leuker dan een lange ketting door het hele klaslokaal te leggen en het zelf te kunnen tellen?
Voordat het kind aan de slag gaat met de korte kralenkettingen moet het in staat zijn om:
- akoestisch te tellen tot honderd
- getallen tot 100 te herkennen
- hoeveelheden tot 100 te herkennen
Maar dit materiaal is niet alleen om te tellen, het kind wordt indirect voorbereid op het werk met machten in Elementary.
Werken met de korte kettingen
De eerste ketting waar het kind mee werkt is de honderd ketting.
Werken met de kettingen bestaat uit:
- De ketting wordt als een lijn uitgelegd op de grond, dit om het kind de volgorde van het lineaire tellen te laten zien.
- Het kind krijgt te zien dat de ketting ook een honderd vierkant is. Hiermee krijgt het kind een indruk van de honderd als vierkant en als lijn en daarmee een indirecte voorbereiding op rekenen met machten. (10 X 10 = 100)
- Het kind telt de ketting en plaats de nummers.
De hand is tijdens dit werk bezig om het kind te helpen dit materiaal in zich op te nemen.
Na deze ervaring is het kind in staat om met alle korte kettingen te werken.



Werken met de lange kettingen
Om de kennis van het kind over lineair tellen te verdiepen, brengen we het samen met het decimale systeem.
Het kind werkte met het gouden materiaal en kent de honderden als een vierkant en de duizend als een kubus.
Met de duizend kettingen ontdekt het kind:
- de duizend als een lijn
- de duizend als 10 honderden
- de duizend als een kubus
Het kind krijgt een indirecte voorbereiding op het werken met kubussen (10 x 10 x 10=1000).
We laten dit het kind zien, maar het kind maakt de ontdekking van dit verband helemaal zelf.
Ze krijgt het gevoel iets buitengewoons te hebben ontdekt.
Door met de andere lange kettingen te werken, zal het kind niet alleen lineair leren tellen, maar ook sprongsgewijs leren tellen. Met de nadruk op elke laatste kraal van een kralenstaafje, als voorbereiding op de vermenigvuldiging.

Het kralenrek in de middenbouw (6-9)
Er is een continue ontwikkeling tussen de middenbouw en de bovenbouw. Kinderen in de middenbouw kunnen en zullen gedurende hun drie jaar niet alle aspecten van deze materialen beheersen. Dit is nooit een probleem, omdat ze nog steeds met exact dezelfde materialen in de bovenbouw kunnen werken.
Als de kinderen starten in de middenbouw weten ze:
- kleuren en getallen
- tellen in stappen (overslaan tellen)
- Hoe de kettingen zich verhouden tot de vierkanten en kubussen.
De kast wordt vooral gebruikt in de 6-9 groep voor het werk van krachten en veelvouden.
“We especially need imagination in science. It is not all mathematics, nor all logic, but it is somewhat beauty and poetry.”
Dr. Maria Montessori
Machten
We introduceren het kralenrek en het werk met machten met een verhaal, een fabel.

Het kralenrek is als een continent, met verschillende koninkrijken. Elk koninkrijk heeft zijn eigen kleur, maar we vinden altijd dezelfde personages in het koninkrijk.
Laten we eens kijken naar het koninkrijk van 5. Dit is de Koning(kubus), Hij is erg belangrijk. Hij is de belangrijkste en heeft de hoogste macht, tot de derde. Er zijn ook prinsen (vierkanten). Ze zijn niet zo belangrijk en ze hebben minder macht - tot de 2de. De edelen, de ridders (kralenstaafje) zijn nog minder belangrijk: tot de 1ste macht. En dan hebben we in dit koninkrijk de gewone burger(een), hij heeft helemaal geen macht - tot de 0-macht. Deze 4 personages kunnen we in alle koninkrijken op ons continent vinden. Laten we eens op ontdekking gaan...
De kinderen zullen het kabinet nu in een ander licht zien en dat zal veel nieuw leren mogelijk maken.

Kinderen zullen dat leren:
- een staafje van 4, vier keer kan worden neergelegd.
- 4 x 4 = 16 = 4².
- Dit is hetzelfde als de korte ketting van 4.
In de lange ketting van 4 vinden we 4 x 4 x 4 = 4² x 4 = 64.
Na dit werk wordt het leren abstracter en dus meer op papier, maar ze kunnen altijd teruggaan naar het kralenrek om hen te helpen.
Het werk van de machten gaat verder..

Veelvouden
Ook gebruiken we de korte en lange kettingen voor de start van het werk met veelvouden.
Als we opnieuw de ketting van 5 nemen, kunnen de kinderen tellen in sprongen:
- 5,
- 10,
- 15,
- 20,
- 25... om een veelvoud van 5 te vinden.
Op deze manier kunnen de kinderen de veelvouden van getallen tot en met 10 onderzoeken.
Later kunnen ze zien wat de gemeenschappelijke veelvouden zijn van verschillende getallen.
- We kunnen de keten van 3 en 6 nemen. Kinderen werken samen om de telling over te slaan.
- Wanneer kom je tot gemeenschappelijke getallen? Deze vormen de gemeenschappelijke veelvouden.
- Hierna gaan ze meer op papier werken, dus wordt het werk weer abstract

Het kralenrek in de bovenbouw (9-12)
In de bovenbouw wordt het duidelijk waar al het werk met de kettingen, vierkanten en kubussen de kinderen op voorbereidt. Ze hebben strategieën herhaald door middel van variatie.
Machten
Met behulp van hun begrip over machten kunnen de kinderen starten met het werk van de kubussen en prisma’s van 2 en 3. Hiermee wordt het abstracte concept van exponentiële groei gepresenteerd nadat de kinderen met kwadraten hebben gewerkt.
Een kubus met de waarde van 1 wordt verheft tot een volgende macht door met 2 of 3 te vermenigvuldigen totdat de zesde macht is bereikt; een nieuwe kubus.











Kwadraten, kubussen en worteltrekken
Bij het kwadrateren zijn de kinderen in staat om vierkanten te analyseren door ze op te delen in kleinere vierkanten en rechthoeken van kralenstaafjes.

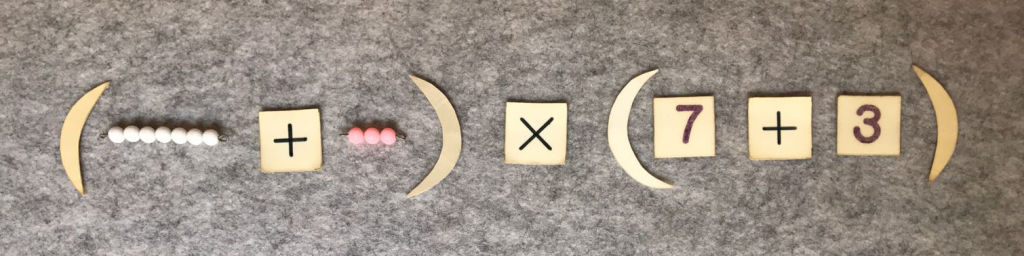
Het kwadrateren van binomen zal helpen om het schrijven dat hoort bij deze vierkanten te bereiken.
De volgende stap is om met meer hiërarchieën te werken. Dit begint met het gouden materiaal (gouden kralen, kralenstaafjes, vierkanten en kubussen) en het eindigt met behulp van hiërarchische knopjes op een knopjesbord die verschillende waarden voorstellen. Een vierkant van veertien ziet er bij deze materialen heel verschillend uit.
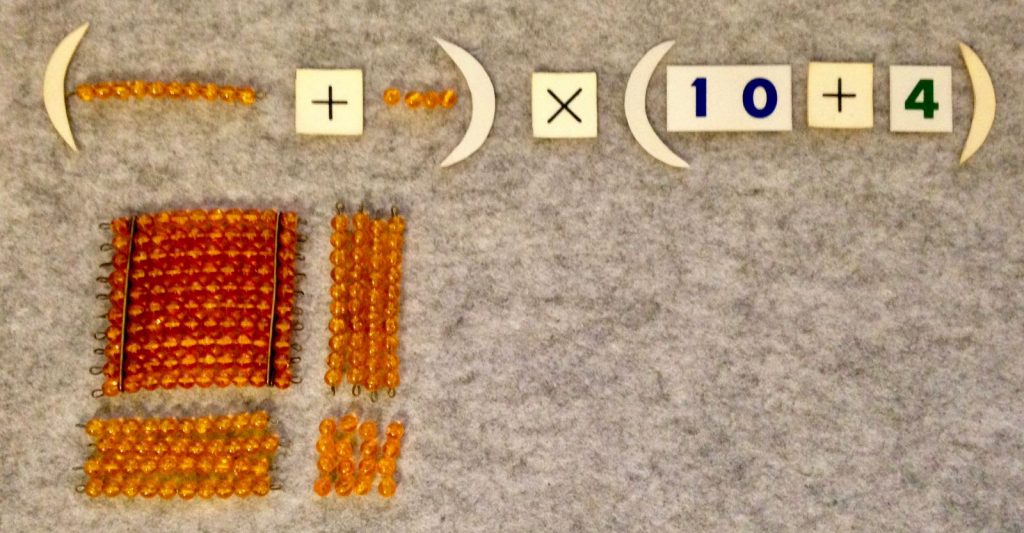

Daarna is het vanzelfsprekend om te beginnen met het omkeren van het proces en te starten met worteltrekken. De kinderen leren de "wortel", "radical" en "wortelteken" kennen. Ook hier kunnen de kinderen de wortel van getallen met maximaal vier cijfers uit de wortel halen, die hen uiteindelijk zal leiden tot enkel schrift.
Het werk van machtsverheffen tot de derde macht en de wortel ervan ziet er ongeveer hetzelfde uit als kwadrateren en de wortel daarvan. In plaats van met de vierkanten te werken, zullen de kinderen de kist met houten kubussen en kwadraten leren kennen.

Hetzelfde werk van analyseren en schrijven zet zich voort en voor de kinderen die er geen genoeg van kunnen krijgen is er de hierarchische kubus voor het werken met meercijferige kubussen en de wortels. De gekleurde kubussen representeren elk een andere hierarchie net als de knopjes voor kwadrateren.
Er is zelfs een algebraische kubus voor de allesweter. En het bijzondere is… dat dit precies dezelfde kubus is waarmee de kinderen sensorisch kennis hebben gemaakt in de onderbouw!

De kubus van 8 (binoom 5 + 3)

De hierarchische kubus

Algebraische trinomische kubus
Geometrie en het kralenrek
Om dit artikel af te sluiten en te laten zien hoe talrijk de mogelijkheden van alleen al het kralenrek zijn, willen we graag deze foto delen die een indruk geeft hoe het zelfs past in het werk van de geometrie.
We hopen dat u het kralenrek nu in een ander licht ziet en dat wanneer u een van onze klaslokalen betreedt, u het als een aanmoediging zult zien om te blijven ontdekken.
