Written by Maaike Steijlen, Zillah de Groot and Marcella Plukaard

Mathematics in Montessori
Maria Montessori interpreted math as just another way of communication between people. With both language and understanding of numbers, human beings started to organize and form civilizations. They are the basis of all understanding we have of this world.
The math materials in a Montessori classroom are mesmerizing materials that unconsciously leads the child in a concrete way to abstraction. The ease with which a child can do mathematics has it roots before the age of 6. With the sensorial material in the Children’s House, they lay their foundation for mathematics later. The 3 to 6 year old child learns through their senses and movement, they need hands on manipulation of the material to learn.
“Never give the mind what has not first been experienced by the hand”
Dr. Montessori
Once in the elementary, the children have the imagination and the wonder to further explore and question what they have learned. Of course, all human beings have a tendency toward order, exactness, precision, estimation, calculation, abstraction, imagination and reason, but the age that children start to really dig deep for answers is during their elementary years.
The bead cabinet is one material in particular that is used in all phases of the Montessori school. From Children’s House until the end of Elementary.
The Bead Cabinet in the Children's House

Children are drawn to the colours and impressiveness of the bead chains. The attractiveness of the material gives the child intrinsic motivation to work with it from a very young age.
There is always a motivation to work up to this material when they see others work with it. Because what is more fun than to lay out a long bead chain throughout the whole classroom and be able to count it by yourself?
Before starting with the chains, the child needs to be able to:
- acoustically count to a hundred
- recognize numbers till 100
- Know quantity till a 100
But this material is not just for counting! The child is indirectly laying the foundation for the work of powers in elementary.
Working with the short chains
The first chain the child is introduced to is the hundred chain.
Working with the chains includes:
- Laying the chain out in a line, to show the child the sequence of linear counting.
- Showing the child the chain can also be a hundred square. With this the child gets an impression of the hundred as a square and as a line and with that an indirect preparation for squaring ( 10 X 10 = 100)
- Counting the chain and place the numbers.
The hand is busy during this work to help the child take this material in.
After this experience, the child is able to work with all short chains.



Working with the Long Chains
To consolidate the child’s knowledge of linear counting we bring it together with the decimal system.
The child has already worked with the golden bead material and knows the hundreds as a square and the thousand as a cube.
With the thousand chain, the child discovers:
- the thousand as a line
- the thousand as 10 hundreds
- the thousand as a cube
The child gets an indirect preparation for cubing (10 x 10 x 10=1000)
This is shown to the child, but the child, all by himself, makes the discovery of this connection now or later in Elementary.
She has the feeling of accomplishing something extraordinary.
By working with the other long chains, the child will go from not only counting in sequence but skip counting with an emphasis on every last bead of a bead bar. This begins their preparation for multiplication.

Bead cabinet or cabinet of powers in the Lower Elementary (6-9)
There is a continuous flow between Lower and Upper Elementary. Children in Lower Elementary do not, and will not be able to master all aspects of these materials during these three years. This is never an issue, as they will still be able to work with the exact same materials in the Upper Elementary.
Starting in Lower Elementary, the children will know:
- colours and numbers
- counting in steps (skip counting)
- How the chains relate to the squares and cubes.
The cabinet is mostly used in the 6-9 group for the work of powers and multiples.
“We especially need imagination in science. It is not all mathematics, nor all logic, but it is somewhat beauty and poetry.”
Maria Montessori
Powers
We introduce the cabinet and the work of powers with a story, a fable.

The cabinet of powers is like a continent, with different kingdoms. Each kingdom has its own colour, but we always find the same personages in the kingdom.
Let’s look at the kingdom of 5. This is the King(cube), He is very important. He is the most important and has the highest power- to the 3rd. There are also princes(squares). They are not as important and they have less power - to the 2nd. The nobles, knights(bead bar)are even less important- to the 1st power. And then in this kingdom we have the common citizen(unit), he has no power at all - to the 0 power. These 4 personages we can find in all kingdoms on our continent. Let’s have a look.
The children will now see the cabinet in a different light and this will open up a lot of new learning.

Children will learn that:
- a bead bar of 4 can be placed 4 times,
- 4 x 4 = 16 = 4².
- This is the same as the short bead chain of 4.
In the long chain of 4 we will find 4 x 4 x 4 = 4² x 4 = 64.
From this point the learning will become more abstract and thus more on paper, but they can always go back to the cabinet to help them.
The work of powers continues…

Multiples
We also use the short and long chains for the start of the work with multiples.
If we again take the chain of 5 we can skip count:
- 5,
- 10,
- 15,
- 20,
- 25... to find multiples of 5.
In this way the children can explore multiples up to 10.
Later they can see what the common multiples are of different numbers.
- We can take the chain of 3 and 6. Children work together to skip count.
- When do you come to common numbers? These will make up the common multiples.
- After this they will move to work on paper.

Bead cabinet in the Upper Elementary (9-12)
In Upper Elementary it becomes clear what all the work of the chains, squares and cubes prepared the children for. They have repeated strategies through variety.
Powers
With their understanding of powers, the older children can start the work with the cubes and prisms for the powers of 2 and 3. This is to show the abstract idea of exponential growth after the children have worked with squaring.
A cube with the value of one is raised to the next power by multiplying by 2 or 3 until reaching the sixth power; another cube.











Squares, cubes and roots
For squaring, the children are able to analyze the squares by taking them apart and by building them up with bead bars and other squares.

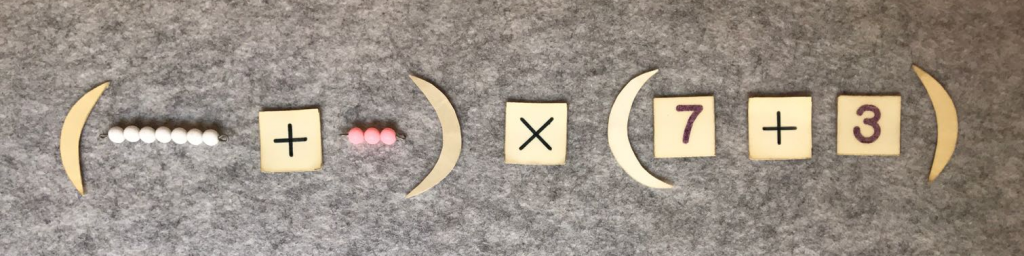
Squaring binomials will then help them to accomplish the writing that belongs with these squares.
The next step is to work with more hierarchies. This starts with the decimal system material (golden beads, bead bars, squares and cubes) and ends using hierarchical pegs on a peg board representing several values. A square of fourteen looks completely different in these materials.
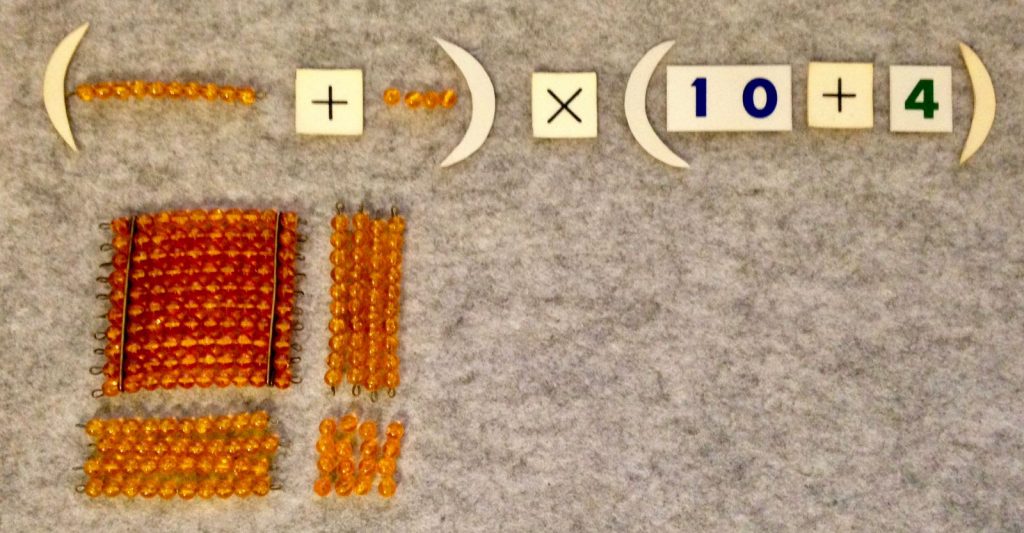

After this, it is only natural to start reversing the process and get into square roots. The children children get to know the “root”, “radicand” and “radical sign”. Again with the peg board, the children will be able to extract the square root of numbers with up to four digits which will eventually lead them into writing only.
The work of cubing and cube root looks much the same like squaring and square root. Instead of working with the bead squares, the children will get to know the wooden cubing material.

The same labor of analysing and writing continues and for the children who just can’t get enough there is the hierarchical cube for working with several digit cubes and cube root. The colored cubes each represent a different hierarchy, as do the pegs for squaring.
There is even an algebraic cube for the know-it-alls. And the interesting thing is… that this is the exact same cube that the children were sensorially introduced to in Children’s House.

The cube of 8 (binomial of 5 + 3)

The hierarchical cube

Algebraic trinomial cube
Geometry and the bead cabinet
To end this article and to show how numerous the possibilities of only this bead cabinet are, we would like to share this picture that reveals how it even fits in with the work of geometry.
We hope that you will never look at the bead cabinet the same way and that when you enter one of our classrooms you will see it as an encouragement to keep exploring.
